12月は冬至の時期で,夕方には早く暗くなります。しかし,昼間の長さが一番短い冬至の日に日の入り時刻が一番早くなるというわけではありません。冬至より10日くらい前が一番早く,冬至のときは日の入り時刻が少しずつ遅くなる時期になります。不思議ですよね。
また,毎日の日の出・日の入り時刻を見ると,昼間の時間が正午(12:00)を境にして午前と午後で対称にならないというのも釈然としません。今回は,この日の出・日の入り時刻について見ていきましょう。
Pythonによる日の出・日の入り時刻の計算
インターネットを見ると日の出・日の入り時刻を計算するサイトがあります。しかし,本ブログでは条件を自由に設定して自分の欲しい物理量を計算し,それをもとに説明したいのでpythonで計算できるようにしました。ChatGPTにコードを書いてもらいました。計算のもとになるライブラリはAstropyで,観測地点や時間を与えると太陽の位置を計算でき,そこから日の出・日の入り時刻などを計算しました。
日の出・日の入り時刻はどの瞬間?
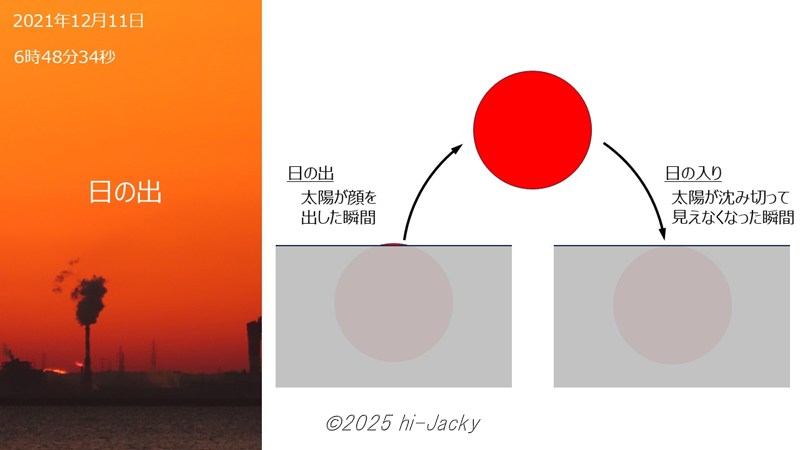
計算で太陽の位置はわかるのですが,どのような状態のときに日の出・日の入りと判断するか決める必要があります。日の出の写真を下に示します。だんだんと日が昇っていきますが,どの瞬間が日の出でしょうか?

太陽の一部でも顔を出した瞬間が日の出です。初日の出を見に行ったとき,太陽が少しでも顔を出せばその瞬間が初日の出だと感じると思います。直感的にもわかりやすいです。
逆に,日の入りは太陽が沈み切って見えなくなった瞬間です。絵で示すと下のようになります。
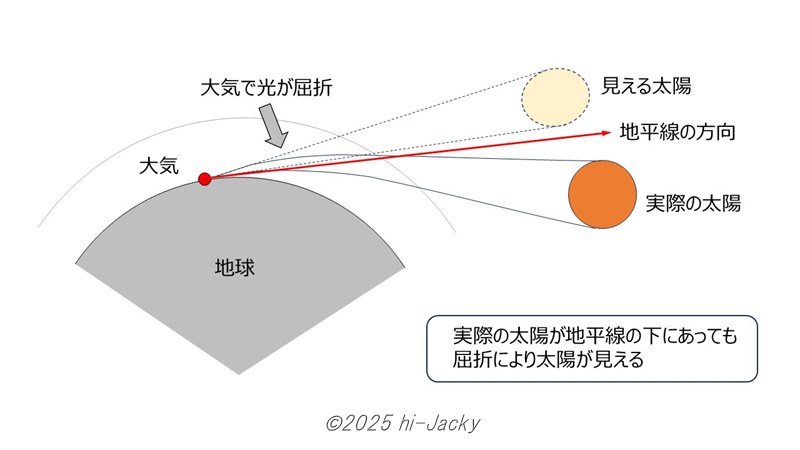
大気のいたずら
ここでひとつ注意することがあります。朝日や夕日の太陽の光は,大気を通ってくるときに屈折して曲げられているということです。大気において空気密度は,高いところでは小さく,地表面に近付くに従い大きくなります。密度が高いほど光の速度が遅いので,下図のように光の経路は上に凸に曲げられます。そのため,実際の太陽が地平線の下にある場合でも,大気の屈折により太陽が見える場合があります。日の出・日の入りのときはこの影響を考慮する必要があります。
今回の計算ではChatGPTの提案した,太陽半径16分(角度),大気差34分(角度)を使い,(16+34)/60=0.833°地平線より低いところに太陽中心がいる場合を日の出・日の入り時刻としました。大気差の値としては他の考え方もあるようなので,皆さんが計算する場合は適宜修正するのが良いかと思います。
参考)暦Wiki/大気/屈折 – 国立天文台暦計算室
東経135°(日本標準時の基準)における日の出・日の入り時刻
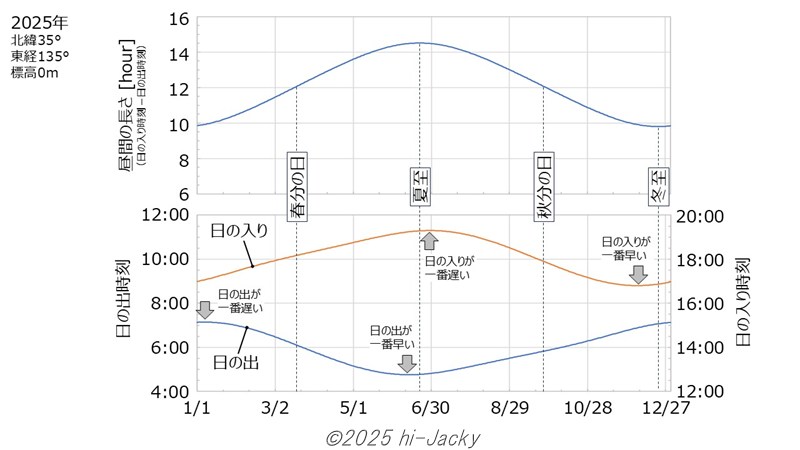
わかりやすくするため日本標準時の基準(子午線)となっている東経135°における日の出・日の入り時刻を計算しました。北緯は35°,標高0mです。また,昼間の長さを「日の入り時刻-日の出時刻」で求めました。
下の図はその結果です。夏至(6/21)で昼間の長さが最も長くなりますが,日の出が最も早いのは6月12日頃,日の入りが最も遅いのは6月29日頃です。夏至のタイミングと1週間ほどずれています。また,冬至については,12月22日で昼間が一番短くなりますが,日の出が一番遅いのは1月7日頃,日の入りが一番早いのは12月5日頃です。冬至のタイミングと2週間以上ずれています。
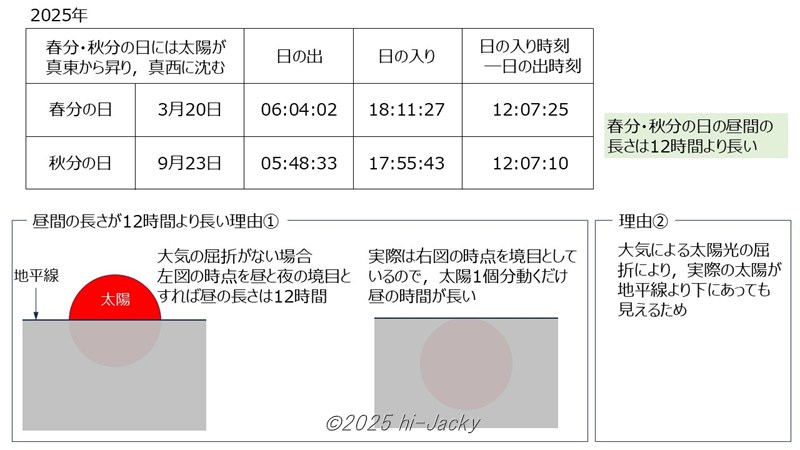
春分の日・秋分の日の昼の長さ
春分・秋分の日を見てみましょう。これらの日は,太陽が真東から昇り真西に沈むので,パッと考えると昼と夜の時間はそれぞれ12時間のように思います。しかし,日の入り時刻と日の出時刻の差から昼間の長さを求めると12時間より7分以上長くなります。この理由を考えましょう。
ひとつ目の理由は,日の出・日の入りをどの時点とするか決めたところに,ふたつめの理由は大気により太陽光が屈折し,実際の太陽が地平線より下にあっても見えてしまうことにあります。
ひとつめの理由を説明します。わかりやすくするために屈折の影響がないと仮定します。昼の長さが12時間になるのは太陽の中心が地平線と重なったときを昼と夜との境目にしたときです。実際には,太陽が顔を出した瞬間や沈み切って見えなくなった瞬間が境目としたので,日の出のときに太陽1/2個分,日の入りのときに太陽1/2個分,あわせて太陽1個分動く時間だけ昼間の長さが長くなります。
午前と午後の昼間の長さ
正午(12:00)を中心にして,午前と午後の昼間の長さを比較してみましょう。
午前の昼間の長さ=12:00-日の出時刻, 午後の昼間の長さ=日の入り時刻-12:00
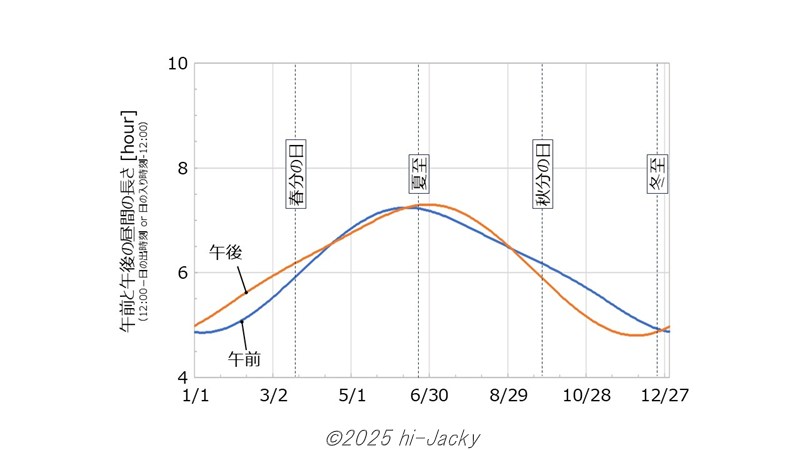
普通に考えると,正午が真ん中で午前と午後の昼間の時間は同じのような気がしませんか? しかし計算してみると(下図),昼間の長さは午前の方が長かったり午後の方が長かったりします。結構複雑で単純でないことがわかります。
まとめ
日の出・日の入り時刻や昼間の長さについて見てきました。結構複雑な挙動をしていて,このままでは何が起こっているのかよくわかりません。次回は,この原因について考えてみたいと思います。


